树状数组

区间信息维护查询

一、二叉索引树(树状数组)（Binary Indexed Tree,BIT)

BIT支持两种操作

1.update(x):修改单点值
2.query(L,R)：查询(L,R)区间和

实现方式：

首先我们介绍一下lowbit(x)

lowbit(x)表示x的二进制表达式中最右边的1所对应的值

程序实现为lowbit(x)={return x&(-x)}

原理就是计算机的整数用补码表示，所以-x就是x按位取反，末尾加1

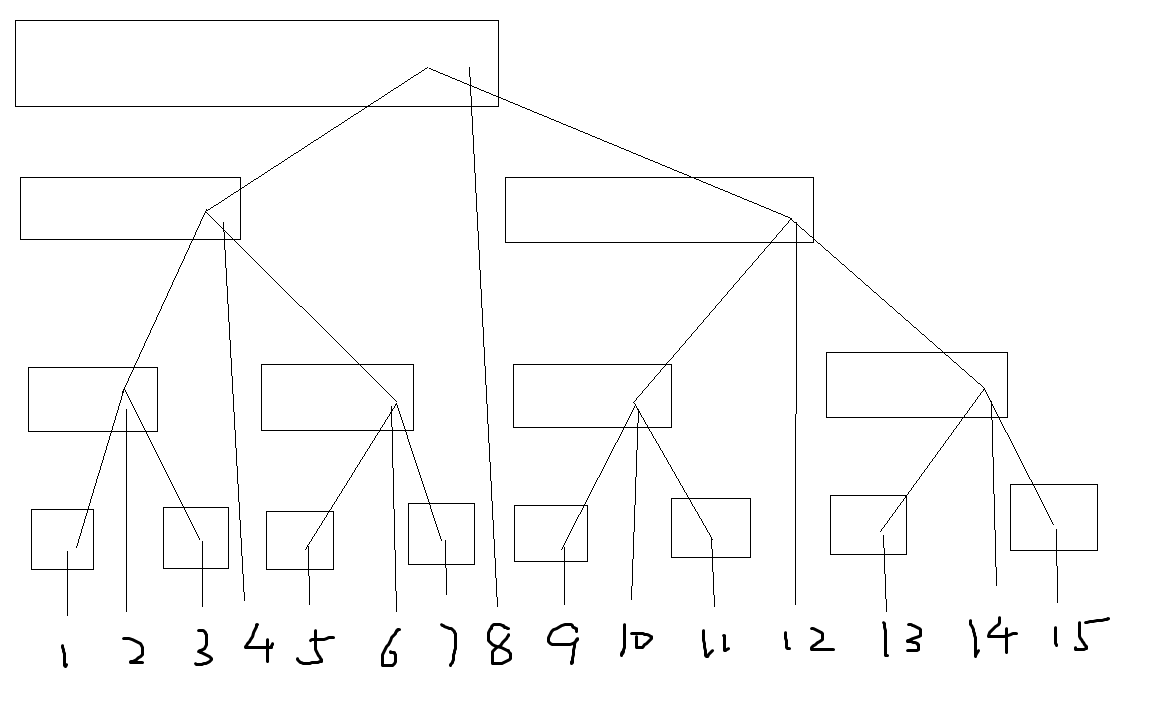
bit示意

上图就是典型的BIT

通过观察我们发现对于节点i,如果i是右儿子,i的父节点为i-lowbit(i),如果i是左儿子,i的父节点为i+lowbit(i).

然后我们构造一个辅助数组C

Ci=Ai-lowbit(i)+1+Ai-lowbit(i)+1+...+Ai

即Ci为区间[i-lowbit(i)+1,i]的和(上图的长方形块)

有了这些准备后我们就要开始思考如何进行add和query的操作

query(L,R):

根据前缀和的思路，我们想到可以分别求出前缀和S[R]和S[L]得到query()的值

以S[L]为例，L以二进制表示，则可以表示为以2为底的幂的和

所以S[L]=Ca+Cb+...+Cz

要实现这一操作，就要从L开始将S[L],S[L-lowbit(L)]...加入S[L]，直到L==0

代码如下

1
2
3
4
5
6
7
8
int sum(int x){
    int ret=0;
    while(x>0){
        ret+=a[x];
        x-=lowbit(x);
	}
    return ret;
}

update(x):

对单一值更新之后，要对包含x的Ci都进行更新

实现操作，要从x向上，直到x>n

1
2
3
4
5
6
void update(int x){
    while(x<=n){
        C[x]++;//更新
        x+=lowbit(x);
    }
}

例题 Ping pong

UVALive - 4329

首先，选手的位置不能改变。而对于某个选手i，假设他为裁判，此时在他之前比他小的有ci个,在他之后比他小的有di个，那么i选手做裁判的情况就有ci(n-i-di)+(i-ci-1) di

问题转换为求ci和di

由小到大遍历1-n，每移动一位就在x[a[i]]++,并求x[a[i]]的前缀和，这是一个经典的BIT问题

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;
const int N=100100;
int a[N],b[N],c[N],d[N];
int n;
int lowbit(int x) {
	return x&(-x);
}
int sum(int x) {
	int ret=0;
	while(x) {
		ret+=b[x];
		x-=lowbit(x);
	}
	return ret;
}
void add(int x,int d) {
	while(x<=N-1) {
		b[x]+=d;
		x+=lowbit(x);
	}
}
int main() {
	int T;
	scanf("%d",&T);
	while(T--) {
		memset(c,0,sizeof(c));
		memset(d,0,sizeof(d));
		scanf("%d",&n);
		for(int i=1; i<=n; i++)scanf("%d",&a[i]);
		memset(b,0,sizeof(b));
		for(int i=1; i<=n; i++) {
			add(a[i],1);
			c[i]=sum(a[i]-1);
			//printf("%d ",c[i]);
		}
		//printf("\n");
		memset(b,0,sizeof(b));
		for(int i=n; i>=1; i--) {
			add(a[i],1);
			d[i]=sum(a[i]-1);
			//printf("%d ",d[i]);
		}
		//printf("\n");
		long long ret=0;
		for(int i=2;i<n;i++){
			ret+=c[i]*(n-i-d[i])+(i-c[i]-1)*d[i];
		}
		printf("%lld\n",ret);
	}
	return 0;
}

总结

BIT本质上还是前缀和，他通过lowbit将前缀和数组拆分，从而使修改的复杂度从O(n)降到O(logn)。从而使动态的区间问题的整体复杂度降至O(nlogn)